【プログラムを作ろう】 ナンプレ編 #4
こんにちは!
エルフィールドでエンジニアとして働いている、H.Tと申します
今回は「ナンバープレイス・プログラム」の第4回目になります。
前回のプログラムでは、行・列の制約を考慮しながら数字を配置する手法をベースに、「マスごとに入れられる数字の候補
(フラグ)」を活用して解法を進めました。
今回は視点を少し変えて、“ブロック単位” での配置を起点にプログラムを組み立ててみます。
🔍 ブロックを出発点にする発想
あれこれ試していて、ふと気づいたことがあります。
それは「特定の3ブロックに限れば、他と干渉せずに数字を自由に入れられる」という点です。
たとえば「左上・中央・右下」の3ブロックを選ぶと、それぞれの9マス内の数字は、他の2つのブロックと被らないため、
自由に 1〜9を並べることができます。(もちろん、ブロック内で重複はNG)
実際には「上中央・右中央・左下」など、同じように独立性のある3ブロックの組合せはいくつか存在しますが、
今回はシンプルに「左上・中央・右下」の構成を採用します。
このように、最初に「自由に数字を入れられるブロック」を固定することで、残りのマスに対しては制約が増し、
完成に近づきやすくなるのでは?という考え方を出発点にします。
🧩 設計の概要
- まず3ブロックに 1〜9 の数字をランダムに配置します
→ 同一ブロック内で重複がなければOK - その後、残りのマスに候補となる数字をチェックし、可能な中からランダムで選んで埋めていく形にします
🛠️ 前回のプログラムで使った「フラグ(isX)」や「状態(done)」の管理処理は流用できるので、新たに追加した部分を
中心に説明していきます。
🔀 配列をランダムに並び替える
まずはブロックに入れる 1~9 の数字をランダムに並び替える関数です
const list19 = [1,2,3,4,5,6,7,8,9]
function getRndlist19(){
return Array.from(list19).sort((a, b) => Math.floor(Math.random() * 2) * 2 -1)
}
📝 ポイント解説:
- Array.from(list19) で元の配列をコピー
- sort() の中にランダムで -1 または 1 を返す関数を使い、並び順をシャッフル
- Math.random() で 0 または 1 を出し、* 2 – 1 によって -1 または 1 を生成しています
これはあくまで簡易的なシャッフル手法ですが、目的には十分です。
⚙️ プログラムの全体構成
実際のコードは以下のようになっています。
<!DOCTYPE html>
<html>
<head>
<title>Number Place</title>
<style>
#app TABLE{border-collapse: collapse;}
#app TD{width: 3rem; height: 3rem; text-align: center; border: solid 1px #CCC ;}
#app TD:nth-child(1), #app TD:nth-child(3n){border-left-color: #333;}
#app TD:nth-child(3n){border-right-color: #333;}
#app TR:nth-child(1) TD, #app TR:nth-child(3n) TD{border-top-color: #333;}
#app TR:nth-child(3n) TD{border-bottom-color: #333;}
</style>
</head>
<body>
<div id=”app”></div>
<script>
const list02 = [0,1,2]
const list08 = [0,1,2,3,4,5,6,7,8]
const list19 = [1,2,3,4,5,6,7,8,9]
function init(){
myTable = document.createElement(‘table’)
list08.forEach(i => {
let tmpTR = document.createElement(‘tr’)
list08.forEach(j => {
let tmpTD = document.createElement(‘td’)
let tmpBlock = ‘b’ + Math.trunc(i/3) + Math.trunc(j/3)
tmpTD.setAttribute(‘class’, (‘r’ + i) + ‘ ‘ + (‘c’ + j) + ‘ ‘ + tmpBlock)
tmpTD.setAttribute(‘done’, 0)
list19.forEach(n => {
tmpTD.setAttribute(‘is’ + n, 0)
})
tmpTR.append(tmpTD)
})
myTable.append(tmpTR)
})
document.querySelector(‘#app’).append(myTable)
}
function getRndlist19(){
return Array.from(list19).sort((a, b) => Math.floor(Math.random() * 2) * 2 -1)
}
function setDisAbleCell(TD){
// 他のマスで数字が置けないようにセットする
let n = TD.innerText //セルに入ってる数字
let tmpClasses = TD.getAttribute(‘class’).split(‘ ‘)
tmpClasses.map( (classx) => {
listTD = document.querySelectorAll(‘.’ + classx)
listTD.forEach(cell => {
cell.setAttribute(‘is’ + n, 1)
})
})
}
function getAbleNum(TD){
// そのマスに可能な数字のリストを得る
let outlist = new Array()
list19.forEach(n => {
if(TD.getAttribute(‘is’ + n) == 0){
outlist.push(n)
}
})
return outlist
}
function checkMustCell(){
// 残りのマスをチェックし、一つしか数が入れられないマスに数を入れる。
let listTD = document.querySelectorAll(“[done=’0′]”)
listTD.forEach(cell => {
let checklist = new Array()
list19.forEach(n => {
if(cell.getAttribute(‘is’ + n) == 0){
checklist.push(n)
}
})
if (checklist.length == 1){
cell.append(checklist[0])
cell.setAttribute(‘done’, ‘1’)
setDisAbleCell(cell)
}
})
}
function setNum(cell, num){
// セルに数字を入れて、他のセルの処理をする。
cell.append(num)
cell.setAttribute(‘done’, ‘1’)
setDisAbleCell(cell)
checkMustCell()
}
function putNumber(){
myTable = document.getElementsByTagName(‘table’)[0]
//まず、左上、中央、右下のブロックに数字を入れてしまう。
list02.forEach(i => { //行方向のブロック番号
let rndlist19 = getRndlist19()
let idx = 0
list02.forEach(j =>{
list02.forEach(k =>{
let cell = myTable.getElementsByTagName(‘tr’)[i * 3 + j].getElementsByTagName(‘td’)[i * 3 + k]
if(cell.innerText == ”){
setNum(cell, rndlist19[idx])
}
idx++
})
})
})
// 残りのマスに数を入れていく
let listTD = document.querySelectorAll(“[done=’0′]”)
listTD.forEach(cell =>{
let ablelist = getAbleNum(cell)
if(ablelist.length > 0){
setNum(cell, ablelist[Math.floor(Math.random() * ablelist.length)])
}
})
}
init()
putNumber()
</script>
</body>
</html>
✅ 実行結果と所感
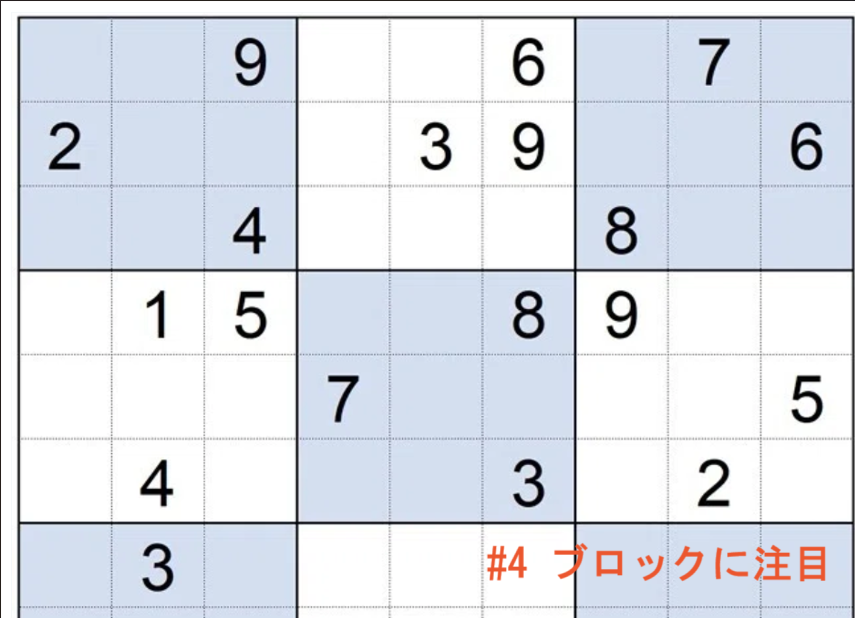
このプログラムを実行すると…
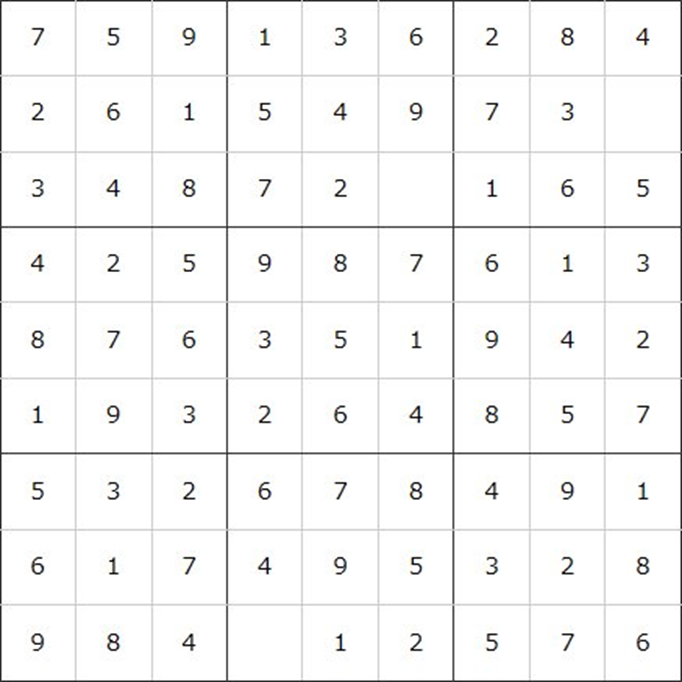
空きマスは残るものの、一定の完成度で盤面が埋まります。
運がよければ…
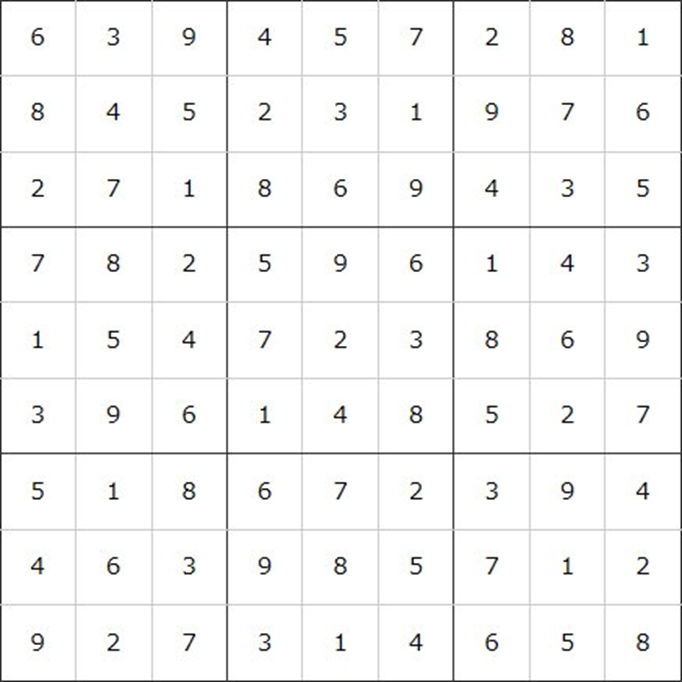
このようにきれいに全マスが埋まることもあります。
🎲 体感的な成功率は4〜5回に1回程度。
まだロジックとしては発展途上ですが、十分に「使える」状態に近づいています。
🤔 気づきと今後の展望
✅ 今回の学び
- ブロック単位の配置は良いスタート地点になる
- 「状態管理(done/isX)」は、今後の検証・アルゴリズム強化に活かせる
- ただし「ランダム選択+制約」だけでは完全な完成は難しい
今回のアプローチでは、特定の3ブロックを起点にすることで「数字の自由度を保ったまま盤面を埋め始める」という、
新たな可能性を見出せました。
ただし、それだけで「全マスを確実に埋める」には至らないことも改めて実感。
やはり「候補数の少ないマスから埋める」「分岐を記録しながら進める」など、より戦略的な要素も必要になってきそうです。
次回は、こうした「埋めた結果を自動で評価する仕組み」を導入して、完成度を上げていく基盤づくりに挑戦していきます!
🔜 次回予告
「現在の盤面が正しいかどうか」を自動でチェックする機能を作ります。
- 重複チェックや不正マスを視覚化
- 今後のステップ(自動生成やパズル化)への足がかりに!
それではまた次回👋
最後までお読みいただき、ありがとうございました!



